دليل دراسة الفيزياء/الحركة

---

علم الحركة

للمزيد من التفاصيل طالع مقالة ويكيبيديا: علم الحركة.

علم الحركة (Kinematics) هو فرع من فروع الميكانيكا (Mechanics) يصف حركة الأجسام والنظم المادية. هناك مفهومان أساسيان لصياغة نظريات علم الحركة بشكلها الكلاسيكي، وهما ثبات الأبعاد المكانية وإسقلاليتها عن الزمن. نستطيع وصف حركة جسم مادي نقطي في فضاء إقليدي باستخدام ثلاثة مفاهيم وهي التنقل، والسرعة والتسارع. بالنسبة للأجسام الحقيقية (التي لا يمكن وصفها بكونها نقاطا رياضاتية)، يصف علم الحركة تنقل ودوران مركز الكتلة (Center of mass) الجسم في فضاء ثلاثي الأبعاد. حاليا سنركز على الحركة الخطية المنتظمة، ثم في وقت لاحق على الحركة الدائرية.

الحركة الخطية

يعرف التنقل، والسرعة والتسارع على النحو التالي.

التنقل

ص. 1- موقع جسم (P) في فضاء ثلاثي الأبعاد.

ص. 2- تمثيل موقع جسم على محور يمثل بعداً واحداً.

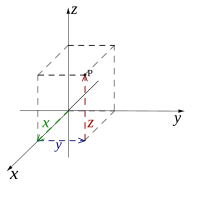
عندما نبحث عن تنقل جسم نسأل هذه الأسئلة "هل غير الجسم موقعه ؟ في أي اتجاه ؟". أول شيء يجب فعله هو تثبيت نقطة مرجعية لدراسة التنقل. يوصف موقع الجسم في الفضاء بإحداثياته الثلاثة (x, y, z) في إطار نظام إحداثي ديكارتي (Cartesian coordinate system) (ص. 1). باستعمال الإحداثيات الديكارتية تكتب متجهة (Vector) التنقل من الأصل إلى نقطة $(x,y,z)$ :

${\vec {r}}=x{\hat {\imath }}+y{\hat {\jmath }}+z{\hat {k}}$

أو

${\vec {r}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}$

$({\hat {\imath }},{\hat {\jmath }},{\hat {k}})$ هي متجهات الوحدة في نظام الإحداثيات الديكارتية.

عندما تتم الحركة في بعد واحد (ص. 2) لنقل على سبيل المثال (x) فإن التنقل هو متجهة، يمكن حسابها كالآتي :

(1.1) $\Delta {\vec {x}}={\vec {x}}_{f}-{\vec {x}}_{i}\,=(x_{f}-x_{i})\,{\hat {\imath }}$

أي أنه الفرق بين الموقع (ونرمز له بالحرف الإغريقي $\Delta$) الذي كان فيه الجسم في النهاية ($x_{f}\,$) وموقعه عند البداية ($x_{i}\,$).

في علم الحركة هناك فرق بين "المسافة" (Distance) و"التنقل" (Displacement)، تخيل أن جسما ما يدور حول مركز؛ المسافة التي يقطعها عندما ينهي دورته هي بكل بساطة محيط الدائرة، ولكن التنقل هو صفر لأنه رجع لنقطة البداية.

السرعة

في علم الحركة، هناك فرق بين "السرعة (Speed)" و"السرعة الاتجاهية (Velocity)". فأما الأولى فهي كمية قياسية (Scalar) وأما الثانية فهي كمية إتجاهية (Vector).

توصف السرعة الاتجاهية المتوسطة (Average velocity) في بعد واحد بأنها نتاج قسمة كمية اتجاهية وهي التنقل، بكمية قياسية وهي المدة الزمنية التي يستغرقها التنقل:

(1.2) $\langle {\vec {v}}\rangle ={\frac {\Delta {\vec {x}}}{\Delta t}}$

وتعرف السرعة الاتجاهية اللحظية (Instantaneous velocity)، حسب حساب التفاضل، على أنها إشتقاق التنقل بالنسبة للزمن:

(1.3) ${\vec {v}}={\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} t}}$

الحرف (d) يعني التنقل الذي يطرأ في فترة متناهية الصغر من الزمن، وهي اختصار للعبارة التالية:

${\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} t}}=\lim _{t\to 0}{\frac {\Delta {\vec {x}}}{\Delta t}}$

السرعة الاتجاهية اللحظية يمكن أن تكون موجبة أو سالبة أو صفرا ووحدتها هي متر \ ثانية (m/s). اما (instantaneuos speed =مطلقInstantaneous velocity

نص عنص عريضريض=== التسارع === "هل يغير الجسم سرعته ؟" يجيب عن هذا التساؤل البحث عن التسارع (Acceleration) أو العجلة.

يعرف التسارع المتوسط، وهو كمية اتجاهية، على أنه معدل تغير السرعة في فترة من الزمن:

(1.4) $\langle {\vec {a}}\rangle ={\frac {{\vec {v_{f}}}-{\vec {v_{i}}}}{t_{f}-t_{i}}}={\frac {\Delta {\vec {v}}}{\Delta t}}$

والتسارع اللحظي هو اشتقاق السرعة الاتجاهية اللحظية بالنسبة للزمن، أي أنه المشتقة الثانية للتنقل:

(1.5) ${\vec {a}}={\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}{\vec {x}}}{\mathrm {d} t^{2}}}$

التسارع اللحظي هو كمية اتجاهية يمكن أن يكون:

• موجباً وهذا يعني أن سرعة الجسم تتصاعد (يعجل).

• سالباً وهذا يعني أن الجسم يبطئ.

• صفراً وهذا يعني أن الجسم إما ساكن أو يسير بحركة منتظمة دون تسارع أو تباطؤ.

وحدة التسارع هي متر \ مربع ثانية (m/s²).

هناك من يستعمل أيضا، خاصة في الملاحة الفضائية، المشتقة الثانية للسرعة وهو ما يعبر عنه بالـزخّة أو التسارع المركب (jerk):

(1.6) ${\vec {j}}={\frac {\mathrm {d} {\vec {a}}}{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}{\vec {v}}}{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}{\vec {x}}}{\mathrm {d} t^{3}}}$

وحدة الـزخّة هي متر \ مكعب ثانية (m/s³).

معادلات الحركة الخطية فے بعد واحد

عندما يسير الجسم بتسارع منتظم، وهذا يعني أن سرعته تزيد بنفس القيمة في فترات متساوية من الزمن، فهذا يعني حسب (مـ 1.6) أن:

${\vec {j}}={\frac {\mathrm {d} {\vec {a}}}{\mathrm {d} t}}=0$

وهذا ما يحدث مثلاً مع السقوط الحرّ للأجسام في حقل الجاذبية الأرضية، فالتسارع ذو قيمة ثابتة. عندما ينطلق جسم في هذه مثل هذه الضروف بسرعة بقيمة سرعة بدائية ($u\,$) لينتهي إلى موقع ما في زمن ($t\,$)، فإن قيمة سرعته النهائية ($v\,$) هي:

(1.7) $v=u+at\,$

وبما أن التنقل الذي يحدث في بعد واحد ($s\,$) بين هاذين الموقعين هو تكامل السرعة، سنتحصل على:

(1.8) $s=s_{0}+ut+{\begin{matrix}{\frac {1}{2}}\end{matrix}}{at^{2}}$

هنا ($s_{0}\,$) هو موقع الجسم عند البداية.

الآن بدمج (مـ 1.7) و(مـ 1.8) ننتهي إلى المعادلة الثالثة للحركة وهي:

(1.9) $v^{2}=u^{2}+2a(s-s_{0})\,$

أو حسب (1.1) على هذا الشكل: $v^{2}=u^{2}+2a\Delta s\,$

هذه المعادلة مفيدة جداً لحساب السرعة عندما لا نمتلك معلومات عن الأوقات.

الحركة الدورانية

ص. 3- وصف الحركة الدائرية.

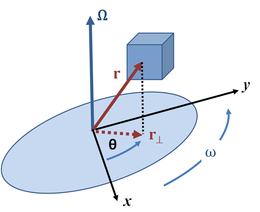
حركة الدوران هي حركة تتم في بعدين على مسار دائري يسمى مداراً. يمكن أن تكون الحركة منتظمة أي أن السرعة الزاوية ثابتة، أو غير منتظمة عندما تتغير السرعة حسب الزمن. يمكن أن يدور الجسم حسب محاور عديدة ولكننا سنختار هنا الحالة التي يدور فيها حول المحور (z).

الموقع الزاوي

المسافة المتجهة من مركز المدار، المنتمي لمحور الدوران، إلى نقطة ما في الجسم الدائر هي متجهة التنقل التي تحدد موقع الجسم (${\vec {r}}$) في كل لحظة من الزمن (ص. 3). هناك إسقاط لهذه المتجهة على المستوي المعامد لمحور المدار نرمز له ب(${\vec {r}}_{\perp }$). الزوية ($\theta$) التي تكونها هذه المكونة العمودية مع المحور (x) هي حسب الاتفاق الموقع الزاوي للجسم الدائر. اصطلاحاً، إذا كان الجسم يتحرك في الاتجاه المخالف لعقارب الساعة فإن الموقع الزاوي يكون موجباً والعكس بالعكس.

وحدة قياس الموقع الزاوي هي الراديان (Radian) إختصاراً (rad).

السرعة الزاوية

المعدل الذي يتغير به الموقع الزاوي حسب الزمن يعرف على أنه السرعة الزاوية ($\omega$). وتكتب قيمة السرعة الزاوية اللحظية كالآتي:

(1.9) $\mathbf {\omega } ={\frac {\mathrm {d} \theta }{\mathrm {d} t}}$

تمثل السرعة الزاوية بمتجهة ( ${\vec {\Omega }}$ ) مطابقة لمحور الدوران حيث تكون قيمتها ($\omega$)، وإتجاهها محدداً بإتجاه الدوران (إلى الأعلى إذا كان الدوران يتم عكس إتجاه عقارب الساعة وإلى أسفل إذا كان الدوران يتم في نفس إتجاه عقارب الساعة).

وحدة قياس السرعة الزاوية هي الراديان \ ثانية (rad/s).

التسارع الزاوي

قيمة التسارع الزاوي ($\alpha$) هي معدل تغير قيمة السرعة الزاوية بالنسبة للزمن:

(1.10) $\mathbf {\alpha } ={\frac {\mathrm {d} \mathbf {\omega } }{\mathrm {d} t}}$

وحدة قياس التسارع الزاوي هي الراديان \ مربع ثانية ($\mathrm {rad/s^{2}}$).

العلاقة بين الكميات الدورانية والخطّية

ص. 4- وصف حركة دائرية بنظام الإحداثيات القطبية.

التنقـل

يحدد تنقل جسم دائر بمتجهة قيماتها اللحظية هي:

(1.11) ${\vec {r}}(t)=R\,{\boldsymbol {\hat {u}}}_{R}(t)\$

حيث (${\boldsymbol {\hat {u}}}_{R}$) هي متجهة وحدة تشير إلى الخارج، من محور الدوران إلى الجسم الدائر. و ($R$) هو نصف قطر المدار.

السـرعة الخطّية

السرعة الخطية لجسم دائر (${\vec {v}}\,$) هي حسب (1.3) تفاضل التنقل بالنسبة للزمن: ${\vec {v}}(t)={\frac {\mathrm {d} }{\mathrm {d} t}}{\vec {r}}(t)={\frac {\mathrm {d} R}{\mathrm {d} t}}{\boldsymbol {\hat {u}}}_{R}+R{\frac {\mathrm {d} {\boldsymbol {\hat {u}}}_{R}}{\mathrm {d} t}}\$

إذا إعتبرنا أن نصف قطر المدار ($R\,$) ثابت طيلة الوقت، فإن المكونة الشعاعية للسرعة (${\vec {v}}_{\perp }$) هي صفر. وبما أن (${\boldsymbol {\hat {u}}}_{R}$) هي متجهة وحدة ذات قيمة ثابتة فإن تغيرها مع الوقت لا يمكن أن يكون سوى نتيجة دوران هذه الأخيرة على منوال متجهة التنقل (${\vec {r}}$) التي تشير دائما نحو الجسم الدائر (أنظر ص. 4). وهذا يعني أن (${\boldsymbol {\hat {u}}}_{R}$) ترسم قوساً ($\mathrm {d} \theta$) في مقدار من الزمن ($\mathrm {d} t$)، أو بعبارة أخرى:

${\frac {\mathrm {d} {\boldsymbol {\hat {u}}}_{R}}{\mathrm {d} t}}={\frac {\mathrm {d} \theta }{\mathrm {d} t}}{\boldsymbol {\hat {u}}}_{\theta }\$

حيث أن (${\boldsymbol {\hat {u}}}_{\theta }$) هي متجهة وحدة معامدة ل(${\boldsymbol {\hat {u}}}_{R}$) وهي تشير بذلك إلى إتجاه الحركة. وبما أن الجسم يتحرك بسرعة لحظية زاوية مقدارها ($\omega$)، إذن فالتغير في متجهة الوحدة (${\boldsymbol {\hat {u}}}_{R}$) هي نتيجة الجداء الاتجاهي (Cross product) (×) لهذه الأخيرة مع متجهة السرعة الزاوية ( ${\vec {\Omega }}$ ):

${\frac {\mathrm {d} }{\mathrm {d} t}}{\boldsymbol {\hat {u}}}_{R}(t)={\vec {\Omega }}\mathbf {\times {\boldsymbol {\hat {u}}}} _{R}=\omega (t)\mathbf {\boldsymbol {\hat {u}}} _{\theta }\$

إذن السرعة الخطية في كل لحظة هي:

(1.12) ${\vec {v}}(t)=R\,\omega (t){\boldsymbol {\hat {u}}}_{\theta }\$

أو بصيغة أكثر بساطة وذلك بإعتبار الكميات القياسية فقط:

$v=R\,\omega$

الحركة في أكثر من بعد

يقال أن الحركة ثنائية الأبعاد إذا ما كانت تتم في مستوي، وثلاثية الأبعاد إذا ما كانت تتم في الفضاء.

---

<< الفهرس • القوى >>